一、随机试验

试验：含义很广泛的术语，它包含各种各样的科学实验、对某一事物的某一特征的观察也可以叫做试验。例如：

抛一枚硬币，观察出现正面和反面的情况
抛一枚硬币多次，观察出现正面和反面的次数
扔骰子，观察出现的点数
在一批灯泡中，任意抽取一个灯泡，测试其使用寿命

以上的这些例子中，它们有这共同的特点：

在相同的条件下可以重复地的进行
试验得出的结果不止一个，并且实现可以明确试验得出的所有可能得结果(试验结果可以穷举)
试验之前是不能明确会出现哪种结果(结果的不确定性)

具有以上三个特点的试验称之为随机试验，常用E来表示一个随机试验。

二、样本空间、随机事件

2.1 样本空间

对于随机试验，虽然在每次实验前无法确定的试验结果，但是试验的能够得到所有结果是可全部列举出来的。因此对于一个随机试验所有的试验结果组成的集合，称为样本空间，常用S来表示一个样本空间。样本空间中的每一个结果，称之为样本点。

2.2 随机事件

有一个随机试验：在一批灯泡中，测试其使用寿命，称它为试验E，其所有的样本点组成的样本空间为S。假设使用寿命低于500小时的灯泡，属于劣质灯泡。我们记t为灯泡的使用寿命，满足使用寿命 t >= 500 小时的样本点组成的一个集合 A={ t | t >= 500 } 是样本空间S的子集。这样我们称集合A为试验E的一个随机事件，一般简称事件。当且仅当这一子集中的一个样本点出现时，称为事件发生。

由一个样本点组成的单点集，称为基本事件。

如果一个事件在每次试验中必然发生，称为必然事件。

如果一个集合不包含任何样本点，称为空集合，用符号 $\emptyset$ 表示。空集合可以样本空间的子集，但是它在每次试验中都不可能发生，所以 $\emptyset$，称为不可能事件。

2.3 事件运算

假设试验E的样本空间为S，A、B、 $A_k$={k=1,2,3…}是S的子集。

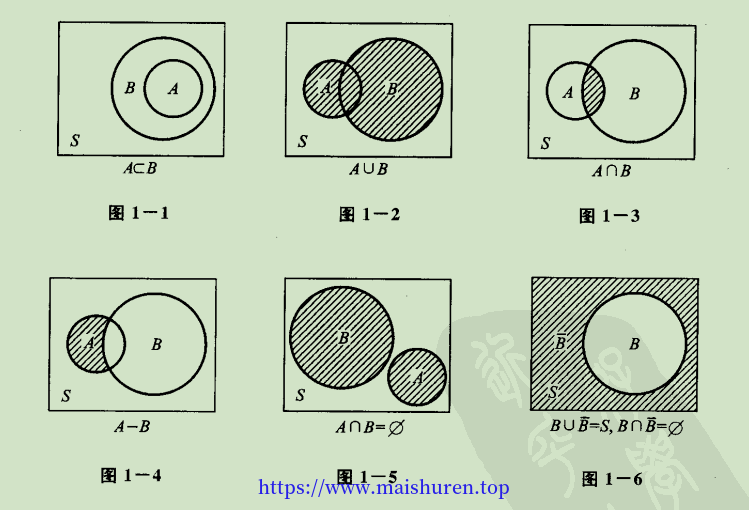
1、如果事件B包含事件A，表示为$A \subset B$。这是指的是事件A发生比导致事件B发生

2、如果 $A \subset B$ 且 $A \supset B$，即A=B，则称事件A与事件B 相等

3、事件 $A \cup B $ = $\set{x | x \in A \text{或} x \in B} $ 称为事件A与事件B的和事件。当且仅当A，B中至少有一个事件发生时，事件 $A \cup B$ 发生

$\bigcup_{\substack{k=1 \}}^{n} A_k$ 为n个事件 $A_1,A_2,A_3,…,An$的和事件，类似的 $\bigcup_{\substack{k=1 \}}^{\infty} A_k$ 为可列个事件 $A_1,A_2,A_3,…$ 的和事件

4、事件 $A \cap B = \set{x| x \in A \text{且} x \in B}$ 称为事件A与事件B的积事件，当且仅当A和B同时发生时，事件 $A \cap B $ 发生，记作 $A \cap B$

类似地，称$\bigcap_{k=1 \}^{n} A_k$ 为n个事件 $A_1,A_2,A_3,…,An$的积事件，称 $\bigcap_{{k=1 \}}^{\infty} A_k$ 为可列个事件 $A_1,A_2,A_3,…$的积事件

5、$A - B = \set{x|x \in A \text{且} x \notin B}$ 称为事件A与事件B的差事件，当且仅当事件A发生，事件B不发生是，事件$A - B$发生

6、如果$A \cap B = \emptyset$ ，则称事件A与事件B互不相容，或互斥。这是指事件A和事件B不可能同时发生，基本事件是两两互不相容的

7、如果 $A \cup B \text{且} A \cap B = \emptyset$，则称事件A与事件B互为逆事件。又称事件A和事件B互为对立事件。这意味着每次实验，要么发生事件A，要么发生事件B。A的对立事件记为：$\overline{A}$。$\overline{A} = S - A$

下图直观地展示了上述中的事件关系和运算。

同样的事件的运算符合交换律、结合律、分配率和德摩根律。

交换律：

$A \cup B = B \cup A$；
$A \cap B = B \cap A$

结合律：

$A \cup (B \cup C) = (A \cup B) \cup C$
$A \cap (B \cap C) = (A \cap B) \cap C$

分配率：

$A \cup (B \cap C) = (A \cup B) \cap (A \cup C)$
$A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$

德摩根律：

$\overline{A \cup B} = \overline{A} \cup \overline{B}$
$\overline{A \cap B} = \overline{A} \cap \overline{B}$

三、频率与概率

3.1 频率的定义

在相同的条件下，进行n次试验，事件A发生次数 $n_A$ 称为事件A发生的频数。比值 $\frac {n_A} {n}$ 称为事件A发生的频率，记为$f_n(A)$。频率具有以下基本性质：

$0\le f_n(A) \le 1$
$f_n(S)=1$
如果$A_1,A_2,..,A_k$是两两互不相容的事件，则：$f_n(A_1 \cup A_2 \cup … \cup A_k)=f_n(A_a)+f_n(A_2)+…+f_n(A_k)$

3.2 概率

由于事件A发生的频率是他发生的次数与试验次数之比，其大小表示A发生的频繁程度。频率大，事件A发生就频繁，这意味着事件A在一次试验中发生的可能性就大。反之亦然。因此直观的想法是用频率来表示事件A在一次试验中的可能性大小。

但是这并不可行，例如“抛硬币”。我们将一枚硬币抛5次、50次、500次等等。当抛硬币的次数较少时，频率波动很大。但随着次数增大，频率会呈现出稳定性，稳定在0.5附近。

设E是随机实验，S是样本空间。对于E的每一事件A赋予一个实数记为$P(A)$，称为事件A的概率，如果集合函数$P(\bullet)$满足以下条件：

非负性：对于每一个事件A，有$P(A)\ge 0$
规范性：对于必然事件S，有$P(S)=1$
可列可加性：设$A_1,A_2,…$是两两互不相容的事件，即$A_iA_j=\emptyset,i\ne j$，$i,j=1,2,…$有$P(A_1 \cup A_2 \cup …)=P(A_1)+P(A_2)+…$

在$n \rightarrow \infty$ (实验次数无穷大)时频率$f_n(A)$在一定意义上接近概率$P(A)$

3.3 概率的一些性质

$P(\emptyset)=0$
令$A_n=\emptyset$(n=1,2,3…)，则$\bigcup_{\n=1}^{\infty}A_n = \emptyset$，且$A_iA_j=\emptyset, i\ne j, i,j=1,2,…$,有概率的可列可加性可得：

$P(\emptyset)=P(\bigcup_{\n=1}^{\infty}A_n)=\sum_{n=1}^{\infty}P(A_n)=\sum_{n=1}^{\infty} P(\emptyset)$

概率具有非负性，所以$P(\emptyset) \ge 0$，所以$P(\emptyset)=0$
由可加性可知，设$A_1,A_2,…$是两两互不相容的事件，即$A_iA_j=\emptyset,i\ne j$，$i,j=1,2,…$有$P(A_1 \cup A_2 \cup …)=P(A_1)+P(A_2)+…$
设A、B是两个事件，如果$A \subset B$，则有$P(B-A)=P(B)-P(A)$; $P(B) \ge P(A)$
对于任一事件A，有$P(A) \le 1$
逆事件的概率：对于任一事件A，有$P(\overline A)=1-P(A)$
加法公式：对于任意两事件A、B，有$P(A \cup B)=P(A) + P(B) - P(AB)$

四、等可能概型(古典概型)

如果一个试验具有以下特点：

试验的样本空间只包含有限个元素
试验中每个基本事件发生的可能性相同

具有以上两个特点的试验，称为等可能概型。它实在概率论早前主要研究对象，所以也称为古典概型。

设试验的样本空间为$S= \set{e_1,e_2,…,e_n}$。因为试验中的每一个基本事件发生的可能性相同，有$P(\set{e_1})=P(\set{e_2})=…=P(\set{e_n})$

因为基本事件两两互不相容，且每一个基本事件的可能性相同，所以，任一基本事件的概率为$\frac 1 n $，证明如下： $$ \begin{align*} 1&=P(S)=P(\set{e_1} \cup \set{e_2} \cup … \cup \set{e_n}) \ 1&= P({e_1}) + P({e_2}) + … + P({e_n}) \ 1&= nP({e_n}) \ {\frac 1 n}&= P({e_n}) \end{align*} $$ 因此可得，设事件A包含k个基本事件，则有 $$ P(A) = \sum_{j=1}^{k} P(\set{e_{i_{j}}}) = \frac k n = \frac {A包含的基本事件数} {S中基本事件的总数} $$ 例1：将一枚硬币抛三次。

1）设事件A为 “恰有一次出现正面”，求P(A)

解法1： $$ \begin{align*} &S=\set{正正正,正正反,正反正,反正正,正反反,反正反,反反正,反反反} \ &A=\set{正反反,反正反,反反正} \end{align*} $$ 因为每一个基本事件的可能性相同，所以$P(A) = \frac 3 8$

解法2：

一共抛3次，每次会出现正反2中结果，所以样本空间S一共有 $222=8$个基本事件。而恰有一次出现正面，第一、第二、第三次个出现一次正面，共3次。所以$P(A) = \frac 3 8$

2）设事件B为 “至少有一次出现正面”，求P(B)

因为$\overline B = \set{反反反}$，所以 $$ P(B) = 1 - P(\overline B) = 1 - \frac 1 8 = \frac 7 8 $$

五、条件概率

条件概率就是在事件A发生的条件下事件B发生的概率，记为$P(B|A)$

例：将一枚硬币抛两次，观察起出现正反面的情况。设事件A为“至少出现以下正”，事件B为“两次都是同一面”。求$P(B|A)$ 事件A发生的情况事件B发生的概率

解：

可以这是个古典概型问题，样本空间$S=\set{正正,反反,正反,反正}，A=\set{正正,正反,反正}，B=\set{正正,反反}$。可见在事件A下出现了事件B一次，所以 $$ P(B|A) = \frac 1 3 $$ 因为事件A限制了事件B，所以可以理解事件A是事件B的样本空间S，因此根据古典概型计算：$P(B|A) = \frac {P(AB)} {P(A)}$ $$ P(A) = \frac 3 4 ,P(AB) = \frac 1 4，P(B|A) = \frac {1/4} {3/4} = \frac 1 3 $$

5.1 乘法定理

有条件概率可得，以下乘法定理：设$P(A) \ge 0$，则有 $$ P(AB) = P(B|A)P(A) $$ 由两个事件可以推广到多个事件的积事件，

$$ P(ABC) = P(C|AB)P(AB)=P(C|AB)P(B|A)P(A) $$

例：设袋子中有 r 个红球，t 个白球。每次从袋子中任取一个球，观察其颜色然后放回，并再放入 a 只与所取出的那只求同色的球。若袋子中连续取球四次，试求第一、第二次取到红球且第三、第四次取到白球的概率。

解：以$A_i(i=1,2,3,4)$表示事件“第i次取到红球”，则$\overline{A_3}$、$\overline{A_4}$分别表示事件第三次、第四次取到白球。所求的概率为： $$ \begin{align*} P(A_1A_2\overline{A_3}\overline{A_4})= \end{align*} $$

概率论基本概念